Quem diz matemática diz demonstração?

Aulus Gellius foi um escritor latino que viveu entre 125 e 180 a.C, na cidade de Attica, na Grécia antiga. Sua obra The Attic Nights, como uma espécie de almanaque, registrou fatos de

sua própria vida, bem comode um tempo anterior ao seu. Ele contou que "(...) o filósofo Favorinus, um pesquisador mais diligente dos registros antigos, afirmou mais positivamente que Arquitas fez um modelo de madeira de uma pomba com tanta engenhosidade e arte mecânicas que voou; estava tão bem equilibrado, como você vê, com pesos e movido por uma corrente de ar fechada e escondida dentro dele." Aulus Gellius repete palavras de Favorinus: “Arquitas, o Tarentino, sendo em outras linhas também mecânico, fez uma pomba voadora de madeira. Sempre que subia, não voltava a surgir." (Aulus Gellius livro XII). Arquitas é hoje considerado o precussor da matemática mecânica. Imagem da wikipedia, da edição latina de 1706, por Jacob Gronovius.

esquema da máquina de architas

Imagem no sítio do Museum of Ancient Greek Technology, onde há uma reconstrução da máquina de voar de Arquitas.

Outros grandes matemáticos posteriores a Pitágoras foram Eudoxo de Cnido (408 a.C a 355 a.C) e seu professor, o pitagórico Arquitas de Tarento (428 a.C a 347 a.C). Possivelmente, Eudoxo e Arquitas tenham vivenciado os primeiros passos do que viria a constituir uma prática matemática descolada do mundo. Plutarco, um historiador grego que viveu no século I (46 d.C. a 120 d.C), se referiu aos dois do mesmo modo, chamando atenção ao caráter prático da matemática (evidências da aderência à vida mundana), mas também ao conhecimento abstrato expresso em palavras e diagramas:
	Eudoxos e Arquitas foram os precursores desta muito famosa e altamente valorizada arte da mecânica, que eles empregaram como uma ilustração elegante de verdades geométricas, e como um meio de sustentar experimentalmente, para a satisfação dos sentidos, conclusões muito complicadas de serem provadas por palavras e diagramas. (Plutarco 1839 p. 697 tradução nossa a partir do inglês)
Plutarco deixou claro também que havia, a esta época, uma declarada oposição a uma apresentação procedural e aplicada da matemática. Nas Simposíacas, Plutarco apontou precisamente uma objeção de Platão com respeito à solução de Arquitas ao problema da duplicação do cubo (dado a medida do lado de um cubo, encontrar a medida do lado do cubo com o dobro da área do primeiro):
	E, portanto, o próprio Platão disgostou de Eudoxus, Archytas e Menaechmus por se esforçarem para reduzir a duplicação do cubo às operações mecânicas; pois, dessa maneira, tudo o que era bom em geometria seria perdido e corrompido, voltando a ser coisas sensíveis, e não elevando-se e considerando imagens imateriais e imortais, nas quais Deus sendo versado é sempre Deus. (Plutarco 2014 livro VIII item 2 tradução nossa a partir do inglês)
Assim, em diversas passagens, fica claro um investimento disciplinar para assegurar um território exclusivo do intelecto para a matemática:
	Mas com a indignação de Platão e suas injúrias contra isto como mera corrupção e aniquilação da boa geometria - que foi, assim, vergonhosamente virando as costas aos não-corpóreos objetos de pura inteligência para recorrer a sensação, e pedir ajuda (que não seria obtida sem subserviência e depravação) à matéria; foi assim que a mecânica veio a ser separada da geometria e, repudiada e negligenciada por filósofos, tomou o seu lugar como uma arte militar. (Plutarco 1839 p. 697 tradução nossa a partir do inglês)

(Heath 1981 p. 247)
A curva de Arquitas foi proposta na busca de solução ao problema da duplicação do cubo. Chama atenção com relação à matemática da época por ser uma elaboração complexa, em três dimensões, envolvendo três superfícies: uma cone à direita, um cilindro, e um toro. A obra On Mathematics Useful for the Understanding of Plato escrita para estudantes de matemática pelo pitagórico Theon de Smyrna (70 a 135 d.C - data estimada) constitui uma fonte preciosa de informações sobre esse problema. Apresenta a versão de Erastóstenes sobre a motivação do problema, que deixa claro que Platão atribuiu a Deus uma preocupação bem além das questões mundanas:
"Eratóstenes, em sua obra intitulada Platonicus, relatou que os Delianos, ao consultar o oráculo sobre como se salvar da praga, foram prescritos por Deus para construir um altar com o dobro do tamanho daquele que já existia. Eles se perguntavam como alguém poderia fazer um sólido que fosse o dobro do outro. Eles consultaram Platão sobre essa dificuldade. Ele respondeu que Deus enviou esse desafio não porque precisava de dobrar o altar, mas para censurar os gregos por negligenciarem o estudo da matemática e por menosprezarem o valor da geometria."(Theon of Smyrna p.2)
Hoje se sabe que esta resolução é impossível com régua e compasso. Isto não significa que só possa ser realizada em matemática abstrata. De fato, há uma resolução com dobraduras.
Além de esclarecer a conjuntura de enunciação do problema, o relato de Eratóstenes mostra que os textos didáticos daquele tempo não isolavam o problema matemático do seu contexto de enunciação.

vaso antigo pintado com imagem das Tesmoforiantes

Nos festivais em homenagem a Dionísio, o Deus das festas, ocorriam competições de tragédias e, a partir de 486 a.C (Aristophanes p.xix), de comédias. As comédias de Aristóphanes, repletas de críticas social e política, nos permitiram reconstruir parte do cotidiano Ateniense do século V a.C. A figura mostra uma cena de As Tesmoforiantes, encenada em 411 a.C. O enredo aborda uma reunião exclusiva de mulheres onde Eurípedes seria julgado pelo tratamento dado às mulheres em suas tragédias. A imagem retrata o vaso do Museu Martin von Wagner - Würzburg, Alemanha.

	N’A República de Platão (428 a.C a 348 a.C) podemos conferir a afirmação de Plutarco, a defesa de uma matemática como “o conhecimento do que existe sempre, e não do que nasce e perece”, ou seja a matemática desprendida do mundo:
		Sócrates — Ora, nenhum daqueles que sabem um pouco de geometria nos contestará que a natureza desta ciência é rigorosamente oposta à que empregam os que a praticam. Glauco — Como assim? Sócrates — Não há dúvida de que essa linguagem de que se utilizam é muito ridícula e miserável. E como homens de prática que fazem as suas afirmações, que falam de esquadriar, de construir, de acrescentar, e que fazem ouvir outras palavras similares, quando toda esta ciência não tem outro objeto além do conhecimento. Glauco — E a mais pura verdade. Sócrates — Não temos de admitir também isto? Glauco — O quê? Sócrates — Que ela tem por objeto o conhecimento do que existe sempre, e não do que nasce e perece. Glauco — É fácil concordar, uma vez que a geometria é o conhecimento do que existe sempre. Sócrates — Portanto, meu dileto amigo, ela atrai a alma para a verdade e desenvolve esse pensamento filosófico que eleva para o alto os olhares que indevidamente baixamos para as coisas deste mundo. (Platão 1997 p.238-239)
	A concepção de Platão com relação à matemática se explica a partir de seu momento de vida, e daí também a concepção geral que ele constrói a respeito do conhecimento e da vida. Observemos, primeiramente, que o texto de Platão é em forma de diálogo, uma transição entre a tradição oral de transmissão de conhecimento filosófico, como fazia o seu mestre Sócrates (469 a.C a 339 a.C), e a tradição formalizada pela escrita, que se efetivará com os escritos de seu discípulo Aristóteles (384 a.C - 322 a.C). Ao fixar as palavras no texto, Platão inicia uma prática de abstração, definindo a forma do argumento. A apresentação dedutiva é uma radicalização máxima deste processo buscando eliminar por completo a fluidez, instabilidade e evasivas da narrativa oral. Mas a transição não se dá somente na expressão literária. Platão viveu a sociedade ateniense em um período de decadência pós-guerras. Ele testemunhou uma época de corrupção, injustiça e descrença no poder estabelecido, a ponto de renderem sátiras nas peças de seu contemporâneo Aristófanes. Em “Pluto, o Deus da Riqueza”, a Pobreza justifica sua própria existência na conduta dos políticos:
		Ora, observa nas cidades os oradores, como eles, enquanto são pobres, são justos com o povo e com a cidade, mas quando enriquecem às custas dos dinheiros públicos, imediatamente se tornam injustos e conspiram contra a plebe e fazem guerra ao povo (Pluto, de Aristófanes).

Platão enxergou no intelecto uma saída para livrar-se deste cenário e alimentar expectativas de tempos melhores. Essas questões presenciadas por ele se refletiram diretamente na sua obra não somente pela escolha do tema central d’A República, que é a justiça, mas também no desenvolvimento de sua abordagem filosófica. Platão depositava no intelecto o caminho para a verdade. Entendia que a sabedoria e a razão livrariam o governo da corrupção e injustiças. Contrapunha o mundo das ideias ao mundo sensível (das sombras). Este último diria respeito a uma esfera subjetiva, a visão humana e sua interpretação sobre as coisas do mundo, algo efêmero, impreciso e incerto. O mundo das sombras poderia também corresponder a um mundo de equívocos e ilusões, como ele relata na alegoria da caverna:

Sócrates — Agora imagina a maneira como segue o estado da nossa natureza relativamente à instrução e à ignorância. Imagina homens numa morada subterrânea, em forma de caverna, com uma entrada aberta à luz; esses homens estão aí desde a infância, de pernas e pescoço acorrentadas, de modo que não podem mexer-se nem ver senão o que está diante deles, pois as correntes os impedem de voltar a cabeça; a luz chega-lhes de uma fogueira acesa numa colina que se ergue por detrás deles; entre o fogo e os prisioneiros passa uma estrada ascendente. Imagina que ao longo dessa estrada está construída um pequeno muro, semelhante às divisórias que os apresentadores de títeres armam diante de si e por cima das quais exibem as suas maravilhas.
Glauco — Estou vendo.
Sócrates — Imagina agora, ao longo desse pequeno muro, homens que transportam objetos de toda espécie, que o transpõem: estatuetas de homens e animais, de pedra, madeira e toda espécie de matéria; naturalmente, entre esses transportadores, uns falam e outros seguem em silêncio.
Glauco — Um quadro estranho e estranhos prisioneiros.
Sócrates — Assemelham-se a nós. E, para começar, achas que, numa tal condição, eles tenham alguma vez visto, de si mesmos e dos seus companheiros, mais da que as sombras projetadas pelo fogo na parede da caverna que lhes fica defronte?

Glauco — Como, se são obrigados a ficar de cabeça imóvel durante toda a vida?
Sócrates — E com as coisas que desfilam? Não se passa o mesmo?
Glauco — Sem dúvida.
Sócrates — Portanto, se pudessem se comunicar uns com as outros, não achas que tomariam por objetos reais as sombras que veriam?
Glauco — É bem possível.
Sócrates — E se a parede do fundo da prisão provocasse eco, sempre que um dos transportadores falasse, não julgariam ouvir a sombra que passasse diante deles?
Glauco — Sim, por Zeus!
Sócrates — Dessa forma, tais homens não atribuirão realidade senão às sombras dos objetos fabricados.
(Platão 1997 Livro VII)

	O Real A tudo que em volta gritava por nomes eu chamava, Real....

Por sua vez o mundo das ideias diria respeito a verdade mais crua. Desvinculado da matéria, as ideias seriam eternas e imutáveis, e alcançáveis através de um raciocínio apurado. Daí a rejeição de uma apresentação da matemática vinculada à prática e a insistência por uma apresentação esquemática, abstrata, um afastamento das coisas corriqueiras (menores) da vida.

Hoje, a acompanhando as propostas dos antigos e as conjunturas em que se formaram, percebemos a impossibilidade de uma ampla compreensão da matemática (bem como de qualquer outro tipo de conhecimento) sem que seja levada em conta uma intrincada rede de relacionamentos que se configura no ambiente onde a matemática é enunciada. Assim, rejeitamos a possibilidade de um conhecimento puro, situado exclusivamente no âmbito das ideias, porque o intelecto já carrega nele próprio as condições conjunturais, e portanto estas questões do tempo e local conformam as próprias ideias. Uma abordagem que não aprofunda as relações presentes no tempo-espaço onde o conhecimento se construiu dá margem a mistérios, coisas inexplicadas e existências autônomas (que surgiram do nada). Por exemplo, o ambiente fértil em ideias que se desenvolveu na Jônia, região que abraçava cidades como Mileto e Samos, de onde vieram Tales e Pitágoras, ainda hoje impressiona historiadores:

		A Jônia, e não a península grega foi o verdadeiro berço da filosofia e da matemática dedutiva. Da Jônia também vieram as grandes obras poéticas de Homero (provavelmente de Samos), a Ilíada e a Odisseia, compostas por volta de 850 a.C. As causas de um dia haver surgido na Jônia uma verdadeira febre intelectual em todas as direções em que o pensamento humano pode se voltar constituem, talvez, o maior mistério da História da Civilização. (Garbi 2007 p.19 grifos do autor)
	Mas o que seria o “maior mistério da História da Civilização” não chegou a surpreender Heródoto. Ao deixar evidentes as demandas daquele povo naquela época, como já foi abordado aqui, a efervescência da vida naquele local explicou o motivo da fertilidade de ideias, desfazendo o mistério.

Sendo as demandas de Platão oriundas da reflexão sobre a sociedade em que vivia, não se espanta que a condução que ele pretendia dar à matemática tenha encontrado acolhimento na mesma sociedade. Assim, acompanhando as demandas conjunturais e a cultura local, a apresentação da matemática foi aos poucos adquirindo traços da organização daquela sociedade. Desde o século VII a.C, as cidades gregas (pólis) contavam com um regime democrático de governo que envolvia os habitantes em processos participativos. Destacam-se em Atenas a Justiça Popular, a Heliéia, criada por Sólon que governou Atenas entre 638 a.C e 558 a.C ou por seu sucessor Clístenes, entre 565 a.C e 492 a.C, e era exercida por um tribunal onde os juízes eram cidadãos escolhidos por sorteio. Eles ouviam a acusação e a defesa e tomavam uma decisão por voto secreto. Além da Justiça Popular, haviam também as Assembleias do Povo, Eclésias criadas por Sólon, em 594 a.C. Todo cidadão ateniense - isso quer dizer homens livres, já que escravos, mulheres e os chamados metecos, estrangeiros que residiam na pólis, não eram considerados cidadãos - podia frequentar as reuniões e votar, bastando levantar a mão. Para isso recebia uma quantia em dinheiro (óbolo) a cada sessão. Essas instâncias da democracia grega eram tão presentes no cotidiano do povo que são retratadas em comédias como “Assembleia das Mulheres”, “As vespas” ou “Pluto”, de Aristófanes escrita em 388 a.C. Por exemplo, num momento em que o pagamento pela participação tinha sido elevado para três óbolos, o coro canta:

Coragem! Tu acreditarás imediatamente no meu ar marcial! Seria uma desgraça se, por causa de três óbolos, andássemos aos empurrões a cada sessão da assembleia. (Pluto, de Aristófanes).

A tradição das assembleias induzia uma arrumação meticulosa nos argumentos de modo a se tornarem convincentes, e esta prática se estendeu aos textos matemáticos. O extremo cuidado com a forma dos enunciados impôs à apresentação da matemática um certo afastamento dos problemas que lhe serviram de inspiração. Aparentando o desprendimento com relação aos problemas do mundo, a matemática foi gradativamente parecendo ser coisa exclusiva do intelecto. Prevaleceu uma apresentação elaborada, lapidada, priorizando o encadeamento (linear), uma matemática dedutiva, que passou a ser confundida com o próprio modo matemático de pensar:

[O método axiomático] não é uma invenção nova; mas seu emprego sistemático como instrumento de descoberta é um dos recursos originais da matemática contemporânea (Bourbaki 2006 p.E.I.8 tradução nossa grifo nosso).

O homem-pássaro, imagem do Metropolitan Museum of Art (US). É descrita como um vaso do século V a.C., na forma de um homem-pássaro provavemente retratando o traje utilizado pelos membros do coro na comédia Os Pássaros de Aristófanes (415/414 a.C.). Mencionando situações cotidianas e personalidades da época, Aristófanes desenvolveu o enredo a partir da história de dois velhos atenienses que resolvem deixar a região na busca de uma cidade sem conflitos e terminam por fundar a Cuconuvolândia (Adriane Duarte 1997).

O papiro P.Oxy. 5299 do lixão de Oxirrinco contém as palavras finais da proposição 4 e início da proposição 5 do segundo livro de Euclides. Estima-se que foi escrito entre 75 e 127 a.C, para uso pessoal, por um escriba não profissional. Embora a imagem não esteja disponibilizada no site POxy: Oxyrhynchus Online pode ser acessada na página de Bill Casselman onde também se pode ver a fotografia da primeira transcrição do papiro. Seguindo a versão da proposição 5 do livro traduzido por Thomas L. Heath, o papiro mostra o seguinte texto: "Se uma linha reta for cortada em segmentos iguais e desiguais, o retângulo contido pelos segmentos desiguais do todo, juntamente com o quadrado na linha reta entre os pontos da seção, será igual ao quadrado na metade." (Heath 1926 p. 382 tradução do inglês).

Um dos mais importantes e mais antigos livros de matemática que se conhece hoje é Os Elementos, de Euclides de Alexandria (330 a.C - ?), escrito por volta de 300 ac. Hoje, não temos mais o texto original. Foram editadas muitas versões, de modo que é preciso ser um estudioso muito especializado para saber verificar as mudanças ao longo das diversas edições e reconhecer algo que se aproxime das intenções da época de Euclides.
De acordo com as traduções que dispomos (Euclides 2009) o texto de Euclides se inicia diretamente em uma sequência de definições, que fixam o significado de alguns conceitos fundamentais, por exemplo, “1. Ponto é aquilo de que nada é parte, 2. Linha é comprimento sem largura, ...”. Ao que parece, não há introdução e nem uma palavra explicativa. Presume-se que as definições, bem como o que vem a seguir nos outros 13 livros que compõem Os Elementos, devam ser suficientemente claros e óbvios ao ponto de dispensar qualquer explicação. Seguem-se às definições uma sequência de noções comuns, que seriam enunciados verdadeiros em qualquer campo. Depois, os postulados, que seriam enunciados evidentes no campo matemático e por fim as proposições, que deveriam ser derivadas diretamente das definições, noções comuns e postulados.
Essa organização parece refletir a concepção de ciência dedutiva formulada pouco antes por Aristóteles, quem já buscava na aritmética e na geometria os termos que se tornariam seus próprios termos técnicos, apropriando-se também de uma ampla diversidade de exemplos matemáticos. Isto tudo serviu, para ele, como exemplo de pensamento necessário ao filósofo (Pereira 2000 p. 60). Na parte do Organon (nome do conjunto de suas obras a respeito da lógica) intitulada Primeiros Analíticos, ele explica o que pretende designar como ciência dedutiva (demonstrativa):
	Devemos, primeiramente, definir o objeto da nossa investigação e o tipo a que pertence. O objeto é a demonstração e o tipo que o realiza é ciência demonstrativa. Devemos a seguir definir uma premissa, um termo, e um silogismo, e a natureza de um perfeito ou imperfeito silogismo; e depois disso, a inclusão ou não inclusão de um termo em outro, assim como em um todo, e o que queremos dizer com predizer um termo de todos, ou de nenhum, ou de outro. (Aristotle p. 81 tradução nossa a partir do inglês).

	Assim, Aristóteles reivindicou para a filosofia o modo esquemático aparentando exatidão e rigor que ele enxergou nas apresentações matemáticas. Seu texto, entretanto, não exibiu diretamente essas características. Embora use letras para representar termos, é ainda repleto de textos explicativos, exemplos, suposições. Completamente diferente do texto que Euclides apresentou n’Os Elementos, que já fez retornar à própria matemática as formas lapidadas pelo filósofo como um modo claro, seco e limpo de pensar.
	Para alguns historiadores da matemática (Boyer 1999 p.71), o que há de novidade n'Os Elementos com relação à matemática da época não são exatamente os resultados matemáticos, mas a capacidade de organizar e expor a informação. Consideram que Euclides se destacava como professor de matemática, não como matemático, já que não apresentou novos resultados.

Trazendo à vista a produção matemática indiana, destacamos outro autor, C. K. Raju que critica o mito da superioridade da matemática formal e do primado grego. Os argumentos de Raju são construídos sobre a consideração do caráter cultural e político da matemática: “A matemática do presente reside em provas formais, que variam com a lógica, mas lógica varia com o tempo, crenças e cultura. Então teoremas matemáticos não são mais do que verdades culturais” (Raju, s.d.). Ele investiga a quem interessa a apresentação dos resultados matemáticos em cda tempo histórico, e portanto, dá visibilidade a uma matemática de compromissos, interesses, uma matemática política.

Mantendo a arrogância de quem julga ter feito primeiro, Raju transfere para a Índia a primazia na produção matemática. Ele argumenta que nunca houve um grego chamado Euclides. Segundo ele, o surgimento desse personagem fictício surgiu dos interesses dos historiadores das Cruzadas e foi mais tarde acolhido, atendendo aos interesses da historiografia moderna da matemática ocidental. De acordo com Raju, as provas em Os Elementos são essencialmente empíricas (não dedutivas), mas havia uma certa conveniência por parte dos filósofos matemáticos do século XX em convencer que Euclides intencionava a escrita de provas dedutivas, mas falhou em seus esforços (Raju 2013). Este ponto é importante porque, como já foi dito aqui, mais tarde, em meados do século XX, o estilo de apresentação da matemática passou a ser identificado também como o modo de pensamento evidenciando um contraste entre a “razão lógica” dos matemáticos e a maneira caótica de pensar das pessoas em geral. Mas Morris Kline deixa claro que

a geometria euclidiana não surgiu desta maneira dedutiva. Levou trezentos anos, período que se estendeu de Tales a Euclides, de pesquisa, tateações e argumentos vagos e até incorretos, até que os Elementos pudessem organizar-se. Por conseguinte, os Elementos constituem o produto acabado e relativamente sofisticado de pensamentos muito mais crus e intuitivos” (Kline 1976 p.53).

Na tradição indiana a matemática não se apresenta com o mesmo rigor e estrutura da matemática ocidental. Ao contrário disso, é expressa em versos, e cantada. A concepção ocidental, que não admite possibilidades outras de construções matemáticas, costuma reduzir o canto (ritmo e rima) a uma estratégia para decorar. No entanto, os indianos têm uma outra explicação. Para eles o canto explicita os vínculos entre a matemática e a vida, uma maneira de deixar evidente as motivações e os propósitos.

	O colar de pérolas de uma mulher é destruído quando ela se envolve no esporte do amor com sua amada. Um terço das pérolas cai no chão. Um quinto vai para debaixo da cama. A senhora arrecadou um sexto e seu amante pega um décimo. A senhora arrecadou um sexto e seu amante pega um décimo. Se seis pérolas permanecerem no próprio fio, quantas pérolas o colar tinha?
Fonte: Great Indian Mathematician - Bhaskaracharya (tradução nossa a partir do inglês) .

Nos interessam n'Os Elementos quarto questões que persistiram na Antiguidade Clássica, na Idade Média, ganharam força no século XVII com as concepções Cartesianas e ainda mais nos tempos modernos, embora apresentando focos de instabilidade:

A primeira questão é a apresentação “seca” e linear das teorias matemáticas. Hoje diríamos: rigorosa e objetiva. É um tipo de apresentação compactada, esquemática, que dá a impressão de que não acrescenta nada ao objeto que pretende comunicar. O livro Os Elementos é escrito em linguagem natural (a linguagem simbólica matemática como conhecemos hoje só vai ser sistematizada na era moderna) mas percebe-se o esforço pela exatidão e clareza. Não tem introdução, nem apresentação e nenhum texto intermediário. Há apenas uma lista de definições, seguida por postulados e noções comuns. Desta lista, Euclides deriva as 465 proposições. Hoje este estilo de descrição matemática é conhecido como método axiomático: parte de um pequeno conjunto de afirmações consideradas evidentes e uma maneira considerada precisa de derivar novas verdades a partir das verdades assumidas ou já derivadas.

O método axiomático atribui à matemática o poder de alcançar, propagar e desvendar a verdade.

A segunda questão é a abordagem reducionista e totalizadora claramente expressa na noção comum de número 8: “o todo é maior do a parte”. Assim, pela junção das partes, configura-se o todo. É essa a estratégia das demonstrações: os mais simples são combinados para formar os mais complexos. Mas não somente isso. O enfoque reducionista também se verifica no esforço de abraçar toda a matemática que se conhecia na época a partir de um conjunto pequeno de regras. Isto demanda a compreensão da matemática como um campo terminado (fechado). Esse ponto de vista torna insuficiente (insatisfatória) qualquer abordagem que não seja tão abrangente quanto a totalidade.

A abordagem reducionista atribui à matemática a garantia o domínio total. Além disso, ao apresentar a matemática como uma totalidade (sem fluxo), situa o matemático no papel de descobridor.

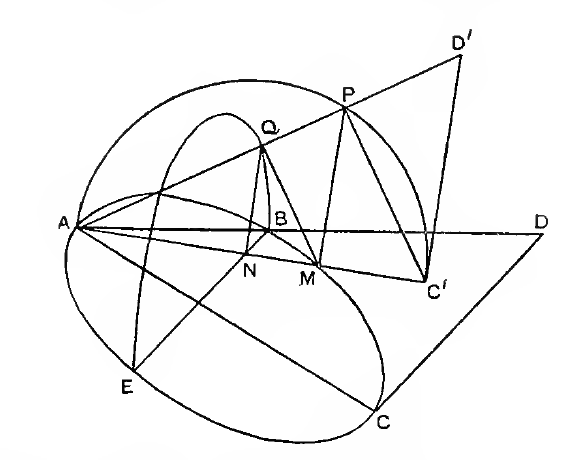
A terceira questão é a intenção de fidelidade ao real. Na época a matemática tinha o papel de permitir a compreensão do mundo real (as percepções mais imediatas), por isso, deveria ser possível conceber a geometria a partir de fatos simples observáveis e intuitivos. Assim, as noções comuns, as definições e os postulados, pontos de partida para a abordagem euclidiana, não são demonstrados nem justificados por serem aderentes à intuição. Entretanto, nos salta à vista a complexidade do quinto postulado em relação aos demais. A presença de um enunciado complexo dentre os postulados levanta a suspeita de que o insucesso no desenvolvimento da demonstração também justificou a designação deste enunciado como postulado, sobrepondo-se ao seu “caráter intuitivo”. Esse assunto relaciona-se com a compreensão Euclideana do espaço. Vejamos:

Postulado 5: E, caso uma reta, caindo sobre duas retas, faça os ângulos interiores e do mesmo lado menores do que dois retos, sendo prolongadas as duas retas, ilimitadamente, encontrarem-se no lado no qual estão os menores do que dois retos. (Euclides p98)

	Sabemos que as concepções aristotélica e platônica já admitiam que a terra fosse esférica. Em "Sobre os Céus", parte 14, escrito em 350 a.C, Aristóteles afirma: “Sobre a posição da Terra e sobre a forma de repousar-se ou movimentar-se, nossa discussão pode terminar aqui. Sua forma é necessariamente esférica” (Aristotle p.916 tradução nossa a partir do inglês). Em “Fédon”, Platão escreve:
		Simmias disse: "O que quer dizer, Sócrates? Eu ouvi muitas coisas sobre a terra, mas certamente não as coisas que te convencem. Eu deveria estar contente de ouvi-las." "Na verdade, Simmias, eu não acho que isso requer a habilidade de Glaucus para lhe dizer o que são, mas provar-lhes que são verdadeiras requer mais do que habilidade de Glaucus, e eu talvez não seja capaz de fazê-lo. Além disso, mesmo se eu tivesse a habilidade, eu acho que minha vida, Simmias, terminaria antes de findar a discussão. No entanto, nada me impede de lhe dizer que o que estou convencido que é a forma da Terra e quais são as suas regiões." "Bem", disse Simmias, "Isso seria suficiente". "Estou convencido", disse ele, "em primeiro lugar de que se a Terra é redonda e no meio do céu, não tem necessidade de ar ou de qualquer outra força para evitar que caia". (Plato s.108d tradução nossa a partir do Inglês).
	Ainda assim, a matemática de Euclides se manteve aderente à intuição mais imediata, o espaço plano observável, onde a menor distância entre dois pontos é a linha reta. Está aqui o motivo de chamarmos “Geometria Plana” à geometria concebida no mundo redondo, e que trata também de volumes curvos, mas é expressa como plana por considerar pequenas distâncias, e o espaço é determinado em três dimensões: altura, largura e profundidade. Isto atendeu às expectativas durante muitos séculos seguintes, alcançando tempos em que interessou à igreja forçar a concepção da terra plana.
	A intenção de fidelidade ao mundo real garantiu à matemática um status de absoluta.
	Mas a partir das grandes navegações, no século XV, quando a Terra voltou a ser redonda: as pessoas viam que, um navio ao se distanciar da costa não despencava no vazio, mas sumia pouco a pouco a partir da base. Passou a ser necessário considerar os cálculos de grandes distâncias, e então, a menor distância entre dois pontos deixou de ser uma linha reta. Daí então toda a concepção de espaço se modificou. A geometria euclidiana já não suportava modelos inspirados no novo mundo. A partir do século XVII as insatisfações com relação ao quinto postulado se tornaram insustentáveis e terminaram por motivar outras geometrias (não euclidianas) que não são planas, mas elípticas ou hiperbólicas (Kubrusly 2016). Novamente aqui, como nas cavernas, como na matemática grega, a percepção do mundo e da vida expressa em conceitos matemáticos.
	A quarta questão é a concepção do espaço como algo fixado, imutável, simétrico, delimitado. Como diz, na definição 1 do livro XI: “O sólido é o que tem comprimento, largura e profundidade”. A geometria euclidiana necessita que o espaço seja fixado e estável para poder ser mapeado (controlado). Os cálculos são precisos, explicados algoritmicamente.
	A matemática controla o espaço, mapeia, conhece e calcula coordenadas.

Cópia da página do livro em que Jeremy Bentham propõe o Panoptico em 1785. Fonte: (Foulcault 2013 fig 17)

Imagem da antiga casa de detenção do Recife, hoje funcionando como Casa da Cultura. O presídio foi construído de acordo com o modelo panótico em 1850. Fonte: Wiki

"O princípio é: na periferia uma construção em anel; no centro, uma torre, a qual possui grandes janelas que se abrem para a parte interior do anel. A construção periférica é dividida em celas, cada uma ocupando toda a largura da construção. As celas têm duas janelas: uma abrindo-se para o interior, correspondendo às janelas da torre; outra, dando para o exterior, permite que a luz atravesse a cela de um lado a outro. Basta então colocar um vigia na torre central e em cada cela trancafiar um louco, um doente, um condenado, um operário ou um estudante. Devido ao efeito da contraluz, pode-se perceber da torre, recortando-se na luminosidade, as pequenas silhuetas prisioneiras na cela da periferia. Em suma, inverte-se o princípio da masmorra; a luz e o olhar de um vigia captam melhor que o escuro que, no fundo, protegia."(Foulcault 2013 p. 319-320)

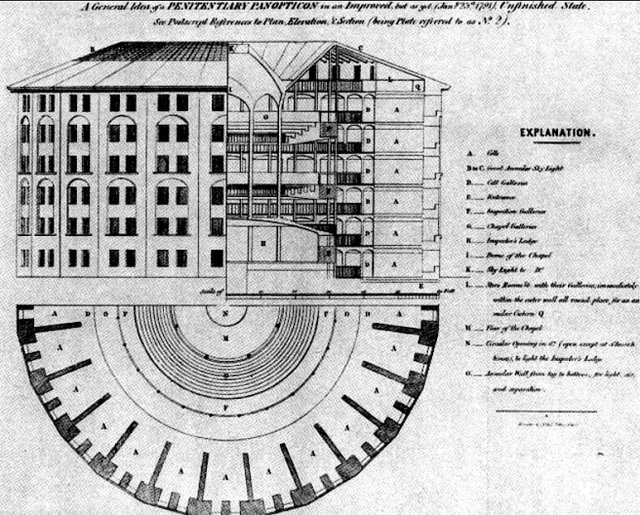
Tempos recentes, na década de 1970, Foucault, no capítulo O Olho do Poder (Foucault 2013), relacionou a compreensão do espaço com as relações de poder no século XVIII. Argumentou que Jeremy Bentham, ao conceber o panóptico reverteu o conceito de vigilância: não mais a escuridão da masmorra (à qual o olho, com o tempo se habitua), mas o olhar atento e totalizante na claridade, o controle (vigilância) centralizado que tudo alcança. Curioso que o panóptico tenha sido proposto por Bentham, que dedicava uma atenção especial às coisas imediatamente vividas, o bem estar imediato, expresso no princípio da utilidade:

Pelo princípio da utilidade se entende aquele princípio que aprova ou desaprova cada ação de acordo com a tendência que pareça ter de aumentar ou diminuir a felicidade da parte cujo interesse está em questão; ou, o que é a mesma coisa em outras palavras, para promover ou para se opor a essa felicidade. (Bentham 1781)..

Para Foucault, o estudo do espaço revela os mecanismos do poder. A proposta utilitarista foi concebida sobre a pretensão do estabelecimento de uma separação precisa entre o bem e o mal, que seria capaz de determinar o aumento ou diminuição da felicidade, e o consequente julgamento das ações entre aprovação ou desaprovação. Se por um lado, este estabelecimento de fronteiras se distancia de uma proposta que acompanha demandas da vida, por outro lado, a matemática da vida, assim como o utilitarismo de Bentham, em seus esforços de solucionar os problemas imediatos, deixam transparecer a concepção de mundo que se tinha em cada época. Os matemáticos também se interessaram pelo espaço, o mapeamento e controle totalizante por coordenadas.

Também na matemática, dominar o espaço significa estabelecer mecanismos de autoridade e poder.

	Referências
	ARISTOPHANES, Clouds. translated by Peter Meineck with introduction by Ian Storey, Hackett Publishing, 2000.
	ARISTÓFANES, Pluto (Riqueza). RAMALHO, A. C. (trad.) Universidade de Coimbra, 1989.
	ARISTOTLE, Prior Analytics, Jenkinson, A. J. (trad.) Disponível aqui.
	ARISTOTLE, On the Heavens, Stoks, J. L. (trad.) Disponível aqui.
	AULUS GELLIUS. The Attic Nights. Trad. Rolfe, John C.. Cambridge. Cambridge, Mass., Harvard University Press; London, William Heinemann, Ltd. 1927. Disponibilizado pelo projeto Perseu aqui.
	BENTHAM, J. An Introduction to the Principles and Morals and Legislation, 1754, Batoche Books Kitshener, 2000, p. 14. Disponível aqui.
	BOURBAKI, N. Éléments de Mathematiques, Théorie des Ensambles. Springer 2006.
	BOYER, C. B. História da Matemática. São Paulo, Editora Edgadr Blücher LTDA,1999.
	DUARTE, Adriane. Palavras aladas: uma pequena teoria do sublime n ’ As Aves de Aristófanes. Língua e Literatura, n° 23, p. 15-27, 1997. Disponível aqui.
	EUCLIDES, Elementos. São Paulo: Unesp. Trad. Irineu Bicudo, 2009.
	FOUCAULT, M. Microfísica do Poder, São Paulo: Editora Graal, 2013.
	FOUCAULT, M. Vigiar e Punir. Nascimento da prisão. Petrópolis: Vozes, 2013.
	GARBI, G. G., A rainha das Ciências, um passeio histórico pelo maravilhoso mundo da matemática, São Paulo: Editora Livraria da Física, 2007.
	HEATH, Thomas. History of Greek Mathematics. Mineola, NY, (EUA): Courier Dover Publications, 1981. Disponivel aqui.
	HEATH, Thomas. The Thirteen Books of Euclid's elements. Vol I. 1926, Cambridge University Press.
	KLINE, M. O fracasso da matemática moderna, trad. Carvalho, L. G. São Paulo: IBRASA, 1976
	KUBRUSLY, R. Geometrias não Euclidianas. Uma breve introdução às Geometrias Hiperbólicas. Disponível aqui. Acesso em: 01 maio 2016.
	PEREIRA, O. P., Ciência e dialética em Aristóteles. Coleção da Biblioteca de Filosofia. São Paulo: Editora Unesp, 2000.
	PLATÃO, A República. Corvisieri, E. (trad.) São Paulo: Editora Nova Cultural Ltda, 1997. Disponível aqui.
	PLATO, Plato in Twelve Volumes, Vols. 5 & 6 translated by Paul Shorey. Cambridge, MA, Harvard University Press; London, William Heinemann Ltd. 1969. Disponível pela Perseus Digital Library.
	PLUTARCO, Marcellus. Plutarch’s Lives. Clough, A. H. (trad.), London, 1839. Project Gutenberg disponível aqui.
	PLUTARCO, Marcellus. Symposiacs. The University of Aelaide, 2014. Disponível aqui.
	RAJU, C. K., Página pessoal na internet. Disponivel aqui.
	RAJU, C. K. Education and the church: decolonizing the hard sciences, 2013. Disponivel aqui.
	Theon of Smyrna (Platonic Philosopher)Mathematics useful for understanding Plato. Translated from the 1892 Greek/French edition by Robert and Debora Lawlor. Wizard Bookshelf, San diego, 1979.

Programa de Pós-Graduação em
História das Ciências e das Técnicas e Epistemologia
UFRJ

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License